El tenis es un deporte apasionante que combina técnica, estrategia, preparación física y, aunque no siempre lo percibamos, una fuerte base matemática. Cada punto, cada juego y cada set se convierten en pequeños experimentos de probabilidad que determinan las opciones de un jugador para imponerse en un partido. Comprender las matemáticas del tenis no solo ayuda a los entrenadores y analistas, sino que también ofrece a los aficionados una mirada más profunda sobre cómo se construyen las victorias.
En este artículo exploraremos cómo las matemáticas se aplican al tenis, desde la probabilidad de ganar un punto hasta los cálculos más complejos que determinan la probabilidad de ganar un partido completo.
1. El tenis como sistema probabilístico
El tenis tiene una estructura jerárquica: los puntos se agrupan en juegos, los juegos en sets y los sets en partidos. Para ganar un encuentro, un jugador debe ir avanzando en cada nivel. Esto convierte al tenis en un sistema acumulativo: ganar un punto no garantiza un juego, y ganar un juego no asegura un set. Sin embargo, cada punto incrementa la probabilidad de lograr esos objetivos mayores.
Aquí es donde entra en juego la probabilidad: si conocemos la probabilidad de que un jugador gane un punto al servicio o al resto, podemos estimar sus posibilidades de ganar un juego, un set y, finalmente, un partido.
2. Probabilidad de ganar un partido
Probabilidad de ganar un punto
El punto es la unidad más básica. Cuando un jugador saca, suele tener una ventaja estadística: el servicio es uno de los golpes más determinantes del tenis.
Los porcentajes varían según el nivel: en el circuito profesional, un buen sacador puede ganar entre el 65% y el 80% de los puntos con su primer servicio. Imaginemos que un jugador A tiene un 70% de probabilidad de ganar un punto con su saque. Ese número, aparentemente simple, es el punto de partida para construir todo el modelo probabilístico del partido.
De forma científica
Cada punto en tenis puede considerarse un ensayo de Bernoulli con probabilidad p. La independencia entre puntos es un supuesto común en los modelos (aunque discutible, pues ignora factores psicológicos y de fatiga).
- p = probabilidad de que el jugador A gane un punto al servicio.
- q = 1−p = probabilidad de que lo pierda.
- t = probabilidad de que el jugador A gane un punto al resto.
Este parámetro fundamental se estima a partir de estadísticas históricas. En ATP, jugadores con gran saque alcanzan valores de p≈0.75-0.80, mientras que al resto suelen caer a t≈0.30–0.40.
Del punto al juego
Un juego de tenis sigue la secuencia de 15, 30, 40 y ventaja. Esto significa que, para ganar un juego, el sacador debe alcanzar al menos cuatro puntos con dos de diferencia. Aquí entran en juego las matemáticas del proceso de Markov, que permiten calcular la probabilidad de avanzar de un estado (30-15, por ejemplo) a otro (40-15) hasta cerrar el juego.
Ejemplo: "Si el jugador A gana un 70% de los puntos con su saque, podemos calcular que su probabilidad de ganar el juego completo al servicio ronda el 90%. Con un porcentaje más bajo, digamos 55%, la probabilidad de mantener el saque cae de forma notable, situándose cerca del 60%."
De este modo, pequeñas variaciones en la probabilidad de ganar un punto generan cambios drásticos en la probabilidad de ganar un juego.
De forma científica
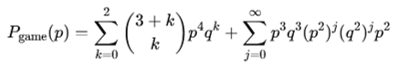
- Si p=0.70, se obtiene Pgame≈0.90
- Si p=0.75, se obtiene Pgame≈0.94
Del juego al set
Un set, en formato tradicional, se gana con 6 juegos con al menos 2 de diferencia, o bien con un tiebreak en caso de 6-6. Las matemáticas aquí son más complejas, porque no solo interviene la probabilidad de ganar al servicio, sino también la de romper el saque del rival.
Ejemplo: "Supongamos que el jugador A tiene un 90% de probabilidad de mantener su servicio y un 20% de romper el servicio del rival. Con estas cifras, las simulaciones muestran que A ganará un set en torno al 70% de las veces."
Lo interesante es que los sets funcionan como bloques estadísticos: aunque se pierda un juego, la probabilidad de ganar el set no desaparece, porque siempre hay nuevas oportunidades de romper el saque contrario.
De forma científica
- s = Pgame(p)
- r = Pgame(t)
Del set al partido
Un partido de tenis puede jugarse al mejor de tres sets (como ocurre en la mayoría de torneos) o al mejor de cinco (como en los Grand Slam masculinos). La probabilidad de ganar un partido se calcula acumulando la probabilidad de ganar sets de forma que si un jugador tiene un 70% de probabilidad de ganar un set, en un formato al mejor de 3, su probabilidad de ganar el partido sube al 78%.
En un formato al mejor de 5, esa misma probabilidad de set se traduce en un 87% de ganar el partido. Esto explica por qué los mejores jugadores suelen ser más difíciles de batir en los Grand Slams: la estructura al mejor de cinco reduce el impacto de la variabilidad y favorece al jugador más sólido.
De forma científica
- Mejor de 3 sets: gana el primero en llegar a 2 sets.
- Mejor de 5 sets: gana el primero en llegar a 3 sets.
- Pmatch-3 = L2+ 2L2(1−L)
- Pmatch-5 = L3+ 3L3(1−L) + 6L3(1−L)2
- Si Pset = L = 0.70, entonces: Pmatch-3 ≈ 0.78
- Si Pset = L = 0.70, entonces: Pmatch-5 ≈ 0.87
Esto demuestra matemáticamente por qué los mejores jugadores son más difíciles de derrotar en Grand Slams: el formato a 5 sets reduce el impacto del azar.
3. Ejemplo práctico: Federer vs Nadal
Para ilustrar mejor, supongamos un enfrentamiento hipotético con los siguientes números:
- Federer gana el 75% de los puntos con su saque y el 35% al resto.
- Nadal gana el 70% con su saque y el 40% al resto.
A partir de estos porcentajes se pueden estimar:
- Federer mantiene su saque en el 92% de los juegos.
- Nadal mantiene el suyo en el 89% de los juegos.
La diferencia parece pequeña, pero acumulada en un set y un partido completo puede ser decisiva. Un ligero 3% de ventaja en los juegos de servicio puede traducirse en un 10-12% de ventaja en la probabilidad de ganar el partido.
4. El azar y la importancia de los puntos clave
Aunque las matemáticas ofrecen modelos precisos, el tenis también está marcado por la psicología y el azar.
- Puntos de break: no todos los puntos tienen la misma importancia. Ganar un 70% de puntos al saque no significa nada si los que se pierden coinciden con las bolas de break.
- Tiebreaks: los desempates son escenarios de alta varianza. Incluso jugadores inferiores pueden robar un set si aprovechan un par de puntos clave.
- Rachas y presión: las matemáticas asumen independencia entre puntos, pero en la práctica los jugadores pueden elevar o bajar su nivel en momentos decisivos.
5. Aplicaciones prácticas
Comprender estas probabilidades no es solo un ejercicio teórico:
- Entrenadores: pueden identificar si su jugador necesita mejorar el saque o la devolución.
- Analistas: utilizan modelos probabilísticos para prever resultados de partidos y torneos.
- Aficionados: disfrutan de una perspectiva más profunda sobre lo que ocurre en la cancha.
- Casas de apuestas y estadísticas deportivas: construyen sus cuotas en gran parte a partir de estos cálculos.
El tenis es mucho más que raquetazos y resistencia física: es un deporte profundamente matemático. Cada punto es una probabilidad, cada juego un cálculo y cada set una suma de posibilidades. Pequeñas diferencias en el porcentaje de puntos ganados se convierten en enormes ventajas acumuladas en la probabilidad de llevarse un partido. Por eso los grandes campeones destacan no solo por su talento, sino también por su consistencia en los momentos clave.
Al mirar un partido de tenis desde esta perspectiva, podemos apreciar que detrás de cada golpe late un fascinante mundo de matemáticas, donde el azar, la probabilidad y la estrategia se entrelazan para dar forma al espectáculo.







